Geometric Prime Conjecture
This page hosts the text of the conjecture, supporting images, and links to software that allows you to explore and test the ideas yourself.
The Martini Glass Conjecture (Part I)
Abstract:
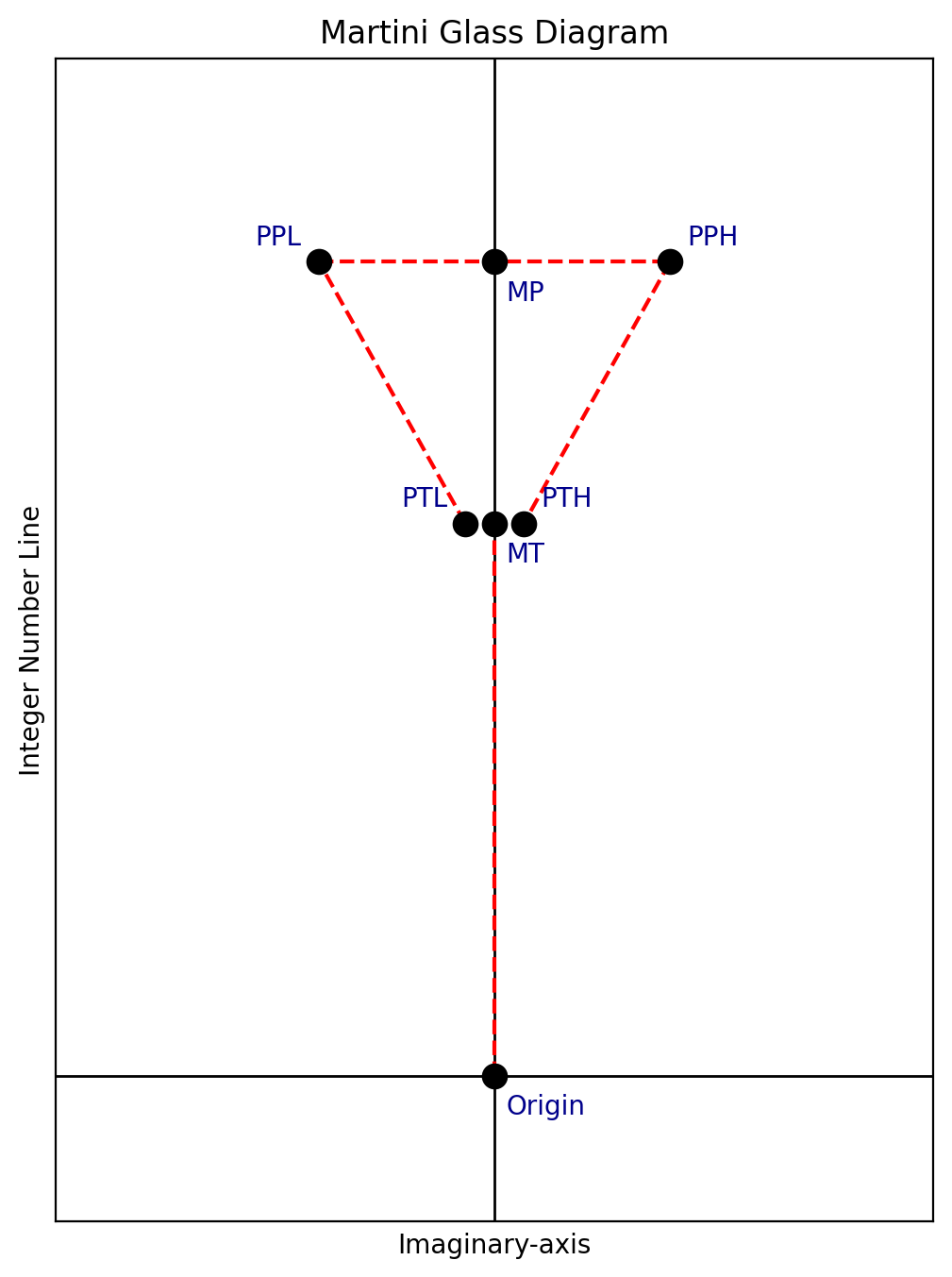
Twin prime midpoints, when expressed as integers, exhibit systematic alignment along well-defined geometric axes. These axes impose numeric constraints on structures assembled from both twin prime midpoints (MT) and prime pair midpoints (MP).
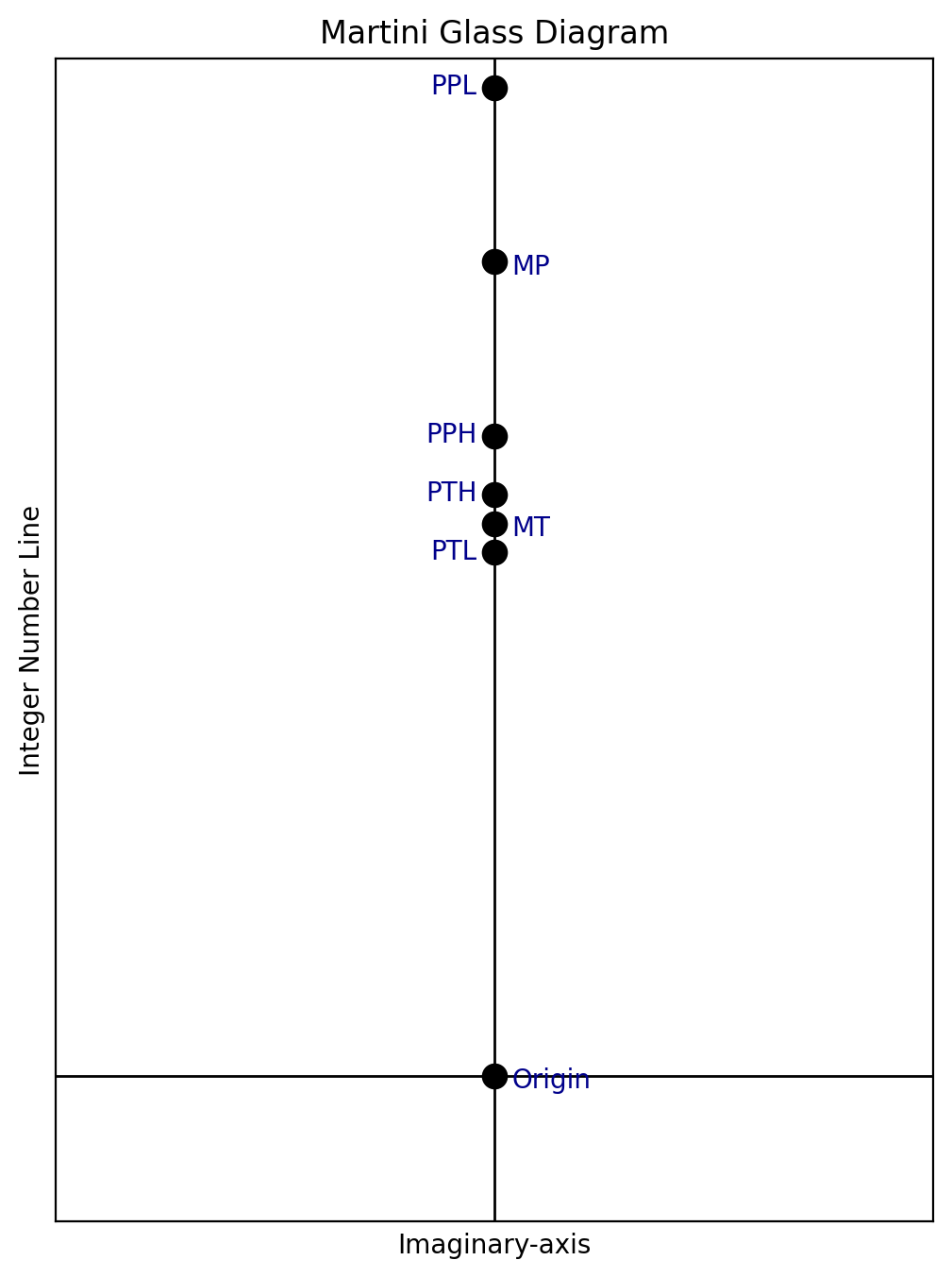
This conjecture identifies groups of four prime numbers—here coined Martini Prime groups, with members denoted PPL, PPH, PTL and PTH—which share a common geometric relationship across scales.
Computational tests up to 10⁸ primes indicate that their occurrence is not random but constrained by deeper field symmetries.
Twin prime midpoints, when expressed as integers, exhibit systematic alignment along well-defined geometric axes. These axes impose numeric constraints on structures assembled from both twin prime midpoints (MT) and prime pair midpoints (MP).
This conjecture identifies groups of four prime numbers—here coined Martini Prime groups, with members denoted PPL, PPH, PTL and PTH—which share a common geometric relationship across scales.
Computational tests up to 10⁸ primes indicate that their occurrence is not random but constrained by deeper field symmetries.
Conjecture:
The midpoint (MP) between consecutive primes is always divisible by a twin prime midpoint (MT), unless:
The midpoint (MP) between consecutive primes is always divisible by a twin prime midpoint (MT), unless:
- The midpoint itself is a twin prime midpoint, or
- The prime gap Δ is itself a twin midpoint or a multiple of a twin midpoint.
Downloadable PDF
📄 Download the Conjecture (PDF)
Supporting Images
Martini Glass Diagram (Vertical)
Martini Glass Diagram (Rotated)
Software Tools
Try running the Python script to check the conjecture on your own machine: